原文地址：

平面方程

平面上的一点以及垂直于该平面的法线唯一定义了 3D 空间的一个平面。

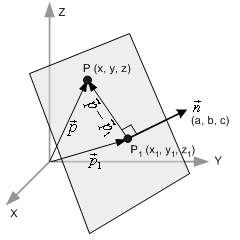
图1 3D空间中的平面

在图一中，给定法线向量 ，以及平面上的一点 P_1，对于平面上的任意一点 P ，我们可以在平面上定义一个由 P₁ 指向 P 的向量：

因为法线 垂直于平面，它必定也垂直于位于平面上的向量 ，因此它们的点积为 0 ：

以上就是平面方程的向量形式，下面我们来看代数形式的，通过点积计算，我们得到：

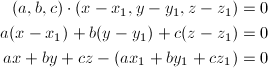
如果我们用 来替代上面表达式中的常数部分，就得到平面方程的代数形式：

原点到平面的距离

如果法线是归一化的，那么平面方程中的常数表达式 d 就是原点到平面的距离。

（图二）平面和归一化法线

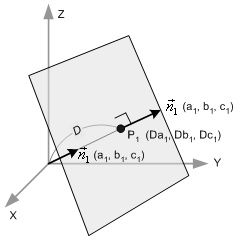
如图二中，给定归一化法线向量 (a₁, b₁, c₁)，以及平面上的一点 P₁ (Da₁, Db₁, Dc₁)，我们来推导原点到平面的距离 D。 将法线向量(a₁, b₁, c₁) 和点 P1 代入平面方程，得到：

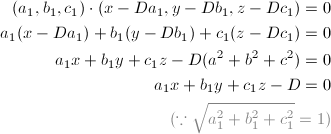
因此，我们可以用标准平面方程除以法线的模（法线长度）来计算原点到平面的距离。举个例子，原点到以 (1, 2, 2) 为法线的平面（x + 2y + 2z - 6 = 0）的距离为 2，计算过程如下：

任意点到平面的距离

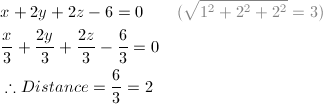
(图三) 任意点到平面的距离

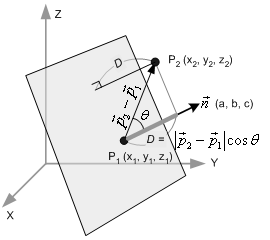
如图三中，我们来推导空间中任意一点 P2 到平面的距离 D 的计算公式。P2 到平面的距离等于由 P1 指向 P2 的向量 在法线向量 上的投影。我们用点积来计算投影距离 D ：

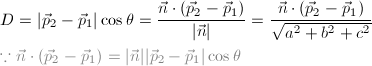
展开分子 ：

代入前面的距离公式，得到最终的点到平面的距离公式：

观察上面的式子，我们就可以发现距离 D 是将点 P2 代入平面方程中，再除以法线的模得到的。举个例子，点(-1, -2, -3)到平面 x + 2y + 2z - 6 = 0 的距离为：

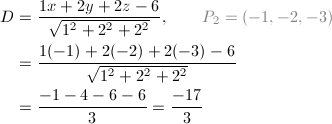
注意：距离是有符号的！它可以为负值，我们可以通过这个符号来决定点位于平面的哪一边(D > 0，点在平面的正面-法线指向那一边；D < 0，带在平面的反面-法线相反方向的那一边，当然 D = 0 就是在平面上啦！)。